Trigonometry is often a terrifying topic for students taking a first calculus class in college. America's trig teaching seems a bit haphazard, and we can't assume students have a good grasp of periodic functions.
This summer project is clearly not offering a full calc curriculum, but instead offering supplemental material. A good lesson on the unit circle is a first step in any college calc discussion of trig. After that, though, students may find practice with a variety of trig problems useful. You can look at particle motion and springs and all sorts of mechanical applications, or you can use a cute and fuzzy animal that also has sharp teeth and claws.... the lynx!
A lot of arctic populations including lynx, snowshoe hare, and lemmings have cyclic population fluctuations and there is a lot of research about why this is. If you've got students in ecology you can ask them to tell you about this in more detail: this is a great topic for a small project or extra credit assignment.
I love this family of examples: there is so much room for discussion of the real world, from foxes and rabbits in my own neighborhood to the wolves and moose of Isle Royale. The examples work so well from precalculus through multivariable, linear algebra, and differential equations. Students can easily experiment with changing parameters in their models, using Excel or more sophisticated programs. And it's all about the circle of life, one of the most compelling stories we as humans know!
Alright then. To the worksheet. I may be a bit dissatisfied with this one yet for reasons I'll outline below. The instructor should display a graph of the actual data, included below. Students then work through
- constructing a trigonometric function from the amplitude and period,
- considering the shape of the actual data as they construct the function, and
- critiquing their model at the end.
As so often is true in modelling, our first instinct -- the sinusoidal function -- is not actually most accurate. If you've got access to the lynx data (you can also find it as a dataset in R, the stats program) you can check that the logarithm of the data is actually more sinusoidal! Look at the long troughs in the the non-log graph, along with the sharper peaks. With students you can use the idea of symmetry to discuss why a sinusoidal approximation is not the best for the non-log-transformed data: the graph does not have reflect-and-glide symmetry, unlike cosine and sine. I, though, honestly don't yet know a good mathematical explanation for the fact that the logarithm of the population data has a more sinusoidal shape. I'd love to hear one.
Worksheet constructing periodic function for lynx trapping
Plot of lynx trapping over time
Plot of logarithm of lynx trapping over time
I know that someone other than me has looked at this blog in the past week! Question of the day: do you use cute fuzzy animals to increase interest and engagement in class?
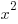and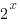 
grow at very different rates. But everyone does that... and I was having fun with atmospheric pressure! This worksheet has a very funky power -- 1/0.19... -- and might be a good way to acquaint students with the messiness of real-life models. I will return to this topic when we get to derivative and integrals, too, because this equation is actually fairly easy to derive.