I'm on a nitrogen kick, I guess. While researching the previous post on beets, which ought to have a follow-up when we get to integration (did you do the worksheet?!), I learned a bit about carbon-nitrogen ratios in compost. The ratio of carbon to nitrogen is important because compost gets hottest when this ratio is around 30:1. Empirical evidence supporting this is not too hard to find, but a mathematical model is hard to find! This is why you need to mix "browns" and "greens" in your home compost.
Again, nitrogen is a very important nutrient for vegetable and grain growth -- if you use up the nitrogen from your soil you'll have small flowers and no tomatoes. Nitrogen conservation in your compost is thus pretty important. But again, I had a hard time finding math equations for this -- unless you count all the cool papers that solved twelve nonlinear systems simultaneously.
Finally, after days of trolling through the library files and becoming much more aware of what a HUGE BUSINESS waste processing is, I found a paper with some polynomials. It's also got some great 3D graphs and some visualizations, in Figure 4, of how these functions depend on their independent variables. Might be food for another post. The authors of "Optimizing composting parameters for nitrogen conservation in composting" took an approach similar to the beet-research people: they did a bunch of experiments, measuring values for aeration of the compost heap, moisture content, particle size, and time after start, and ran a big backward computation to come up with polynomials in those variables (A, M, P, and t) that predicted the carbon/nitrogen ratio (among other things) pretty well. That is the polynomial that the worksheet below focuses on.
This worksheet covers
- related rates, applying the product and chain rules a few times
- physical reasoning: I ask students to examine the assumptions of the model, which I then violate for mathematical purposes!
- and writing English sentences explaining a math result.
Teaching tips: students often freak out about all the symbols in here. Reassure them that many are constants in the problems they're asked to work out. Remind them that the derivative of a constant is zero, even if the constant is one they don't know!
I would like to have had some other "real-life scenarios" or more interpretation, so I'll think about what sorts of related-rates problems could be added to this.
If you've got refinements or modifications, let me know!

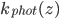
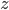
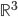
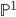
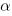 or
or 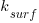 , though they'd prefer to!
, though they'd prefer to!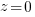 , always a somewhat challenging concept for students. The limit as z goes to infinity can be done with limit rules.
, always a somewhat challenging concept for students. The limit as z goes to infinity can be done with limit rules.